Introduction
Seeing as how the last few posts have been a bit theoretical in nature, I thought it might be useful to switch to something more practical. Early stopping is a strategy used to prevent overfitting, and it works by stopping training once the performance on a validation set becomes worse than the best achieved for some number of epochs. There is a strong assumption going on behind the scenes of this intuitive principle. It assumes that validation accuracy/loss should monotonically increase as we train, and if it doesn’t, we are overfitting our training set. A less obvious but equally important assumption is that there is a strong correlation between loss and accuracy.
When training a neural network that is a discriminative classifier, we typically use the following cross-entropy loss function
\begin{align} \mathrm{L} = - \sum \limits_{i=1}^{N} \sum \limits_{j=1}^{C} t_{ij} \mathrm{log} p_{ij} \end{align}
where \(p_{ij}\) is the probability output by our classifier indicating that sample \(i\) is of class \(j\), and \(t_{ij}\) is $j$th entry in the one-hot vector representation of the \(i\)th label.
CE, like other surrogate loss functions has its flaws, yet one of its biggest flaws is quite subtle: it prefers high confidence predictions. This leaves room for unfavorable scenarios such as a model \(A\) having higher loss than another model \(B\) even though it might have also have higher accuracy. The explanation behind this paradox is that model \(A\) is less confident in its predictions on average than model \(B\).
What does all this have to do with early stopping? Suppose we are training a basic LeNet model on MNIST for 100 epochs, and encounter a figure as seen below.
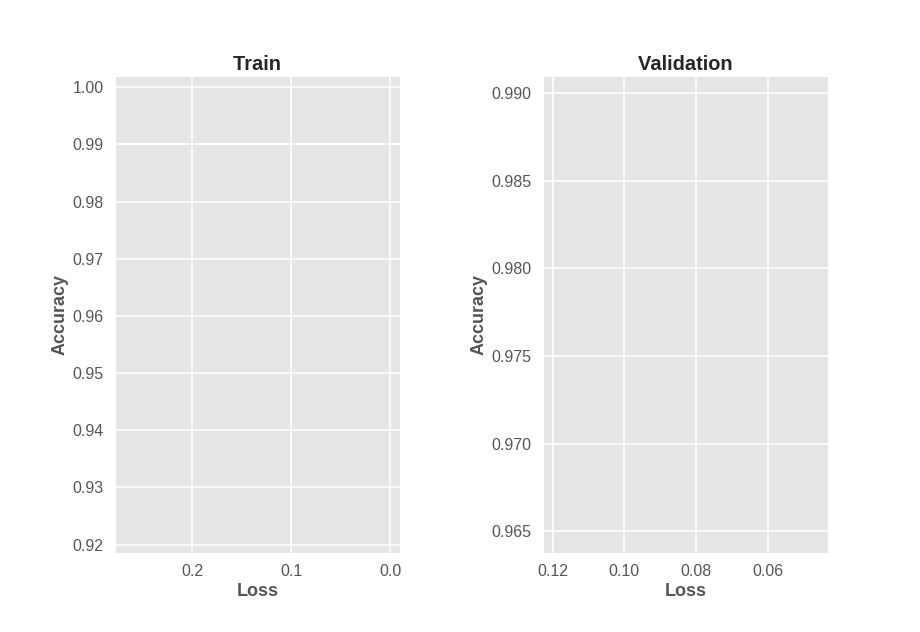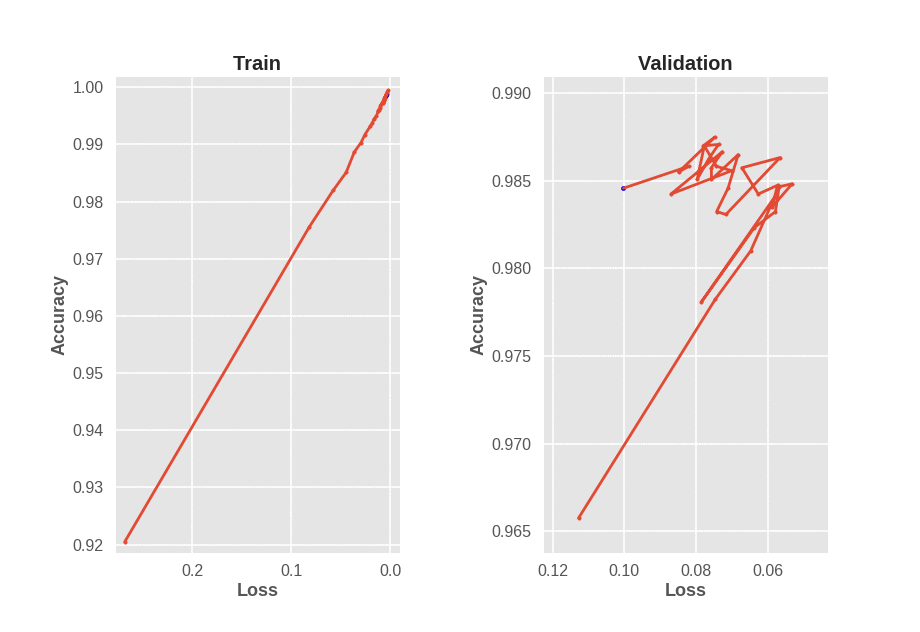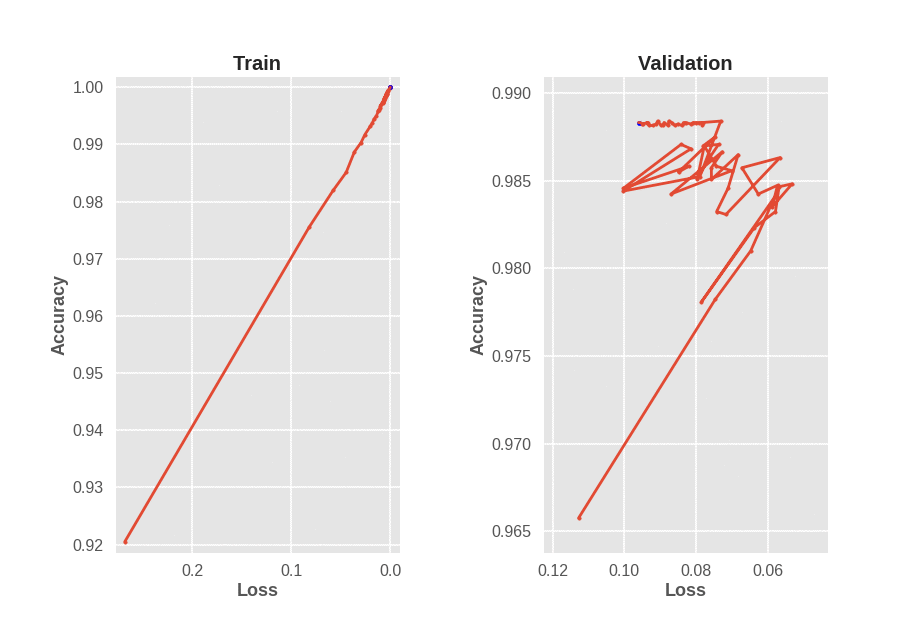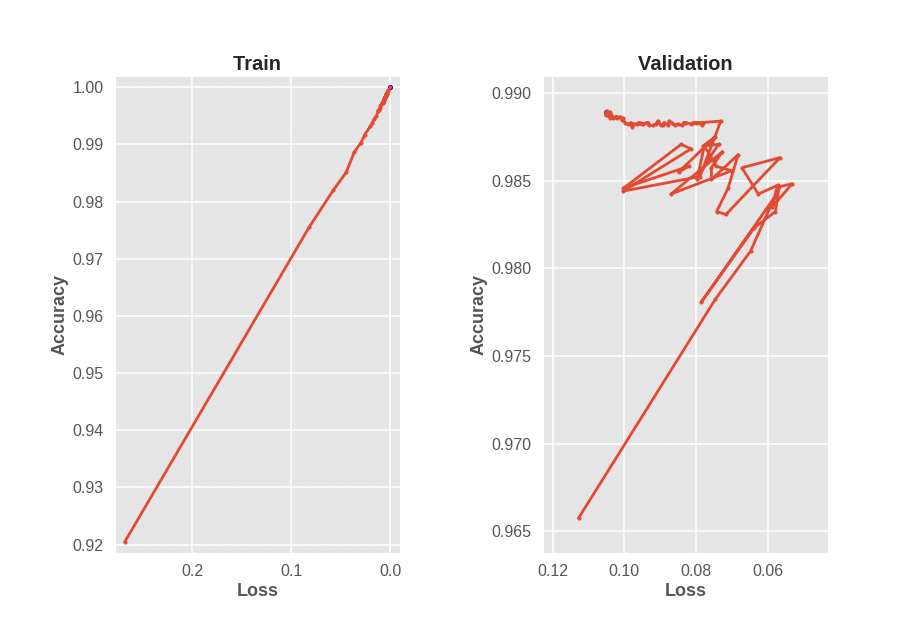
Problems With Early Stopping
Training accuracy monotonically increases as training loss decreases. However, validation accuracy does not monotonically increase as validation loss decreases. This brings up an interesting question. If we train a neural network and see validation accuracy decrease for a while, even though validation loss decreases, should we stop training? We are in fact optimizing loss, not accuracy, so why judge the model based on a metric it wasn’t even desgined to optimize? The figure above suggests that if we are going to use early stopping, we need to simultaneously consider validation loss and validation accuracy. Considering either one without the other assumes a strong correlation between loss and accuracy which simply isn’t a reasonable assumption, at least for CE loss.
Let’s list the 3 possible failure modes of early stopping, and how we attempt to address some of them in this post:
- We track only validation loss as our metric.
- The issue is that validation loss can get worse as validation accuracy improves.
- Can be fixed by considering validation accuracy in addition to validaiton loss.
- We track only validation accuracy as our metric.
- The issue is that validation loss can get better as validation accuracy worsens.
- Questionable if it’s fair to judge a model based on a metric it wasn’t explicitly meant to optimize.
- Can be fixed by considering validation loss in addition to validation accuracy.
- Our notion of best value is too static.
- Perhaps our optimization procedure took too big of a step and now has 2% worse performance compared to the best value encountered up to this epoch. It might take a while for the model to get back on track, so it will be stopped before it is given a chance to improve.
- Can be fixed by considering trends in performance improvement, rather than comparisons to static values.
Point 3 is left for a future post, but we attempt to fix points 1 and 2 by tracking both validation accuracy and loss.
Keras can be very tricky when it comes to enabling reproduciblity when GPUs are involved. Even though I reset numpy and tensorflow seeds between model runs, different results are obtained likely due to cuDNN stochasticity. Note that the best validation accuracy is attained at around 95. Training a model with early stopping based on validation loss results in stopping at around epoch 10. Also, training a model with early stopping based on validation accuracy leads results in stopping at around epoch 13. This is all with a patience setting of 3 epochs, so increasing patience might improve early stopping behaviour, but that’s another hyperparameter to tune. Instead, we modify the EarlyStopping callback in Keras to check progress on mulitple metrics at once.
More Clever Early Stopping
Here is the code for the modified early stopping Callback.
Code
import keras.backend as K
from keras.callbacks import Callback
import numpy as np
class FixedEarlyStopping(Callback):
"""Stop training when a monitored quantity has stopped improving.
# Arguments
monitors: quantities to be monitored.
min_deltas: minimum change in the monitored quantities
to qualify as an improvement, i.e. an absolute
change of less than min_delta, will count as no
improvement.
patience: number of epochs with no improvement
after which training will be stopped.
verbose: verbosity mode.
modes: list of {auto, min, max}. In `min` mode,
training will stop when the quantities
monitored has stopped decreasing; in `max`
mode it will stop when the quantity
monitored has stopped increasing; in `auto`
mode, the direction is automatically inferred
from the name of the monitored quantity.
baselines: Baseline values for the monitored quantities to reach.
Training will stop if the model doesn't show improvement
for at least one of the baselines.
"""
def __init__(self,
monitors=['val_loss'],
min_deltas=[0],
patience=0,
verbose=0,
modes=['auto'],
baselines=[None]):
super(FixedEarlyStopping, self).__init__()
self.monitors = monitors
self.baselines = baselines
self.patience = patience
self.verbose = verbose
self.min_deltas = min_deltas
self.wait = 0
self.stopped_epoch = 0
self.monitor_ops = []
for i, mode in enumerate(modes):
if mode not in ['auto', 'min', 'max']:
warnings.warn('EarlyStopping mode %s is unknown, '
'fallback to auto mode.' % mode,
RuntimeWarning)
modes[i] = 'auto'
for i, mode in enumerate(modes):
if mode == 'min':
self.monitor_ops.append(np.less)
elif mode == 'max':
self.monitor_ops.append(np.greater)
else:
if 'acc' in self.monitors[i]:
self.monitor_ops.append(np.greater)
else:
self.monitor_ops.append(np.less)
for i, monitor_op in enumerate(self.monitor_ops):
if monitor_op == np.greater:
self.min_deltas[i] *= 1
else:
self.min_deltas[i] *= -1
def on_train_begin(self, logs=None):
# Allow instances to be re-used
self.waits = []
self.stopped_epoch = 0
self.bests = []
for i, baseline in enumerate(self.baselines):
if baseline is not None:
self.bests.append(baseline)
else:
self.bests.append(np.Inf if self.monitor_ops[i] == np.less else -np.Inf)
self.waits.append(0)
def on_epoch_end(self, epoch, logs=None):
reset_all_waits = False
for i, monitor in enumerate(self.monitors):
current = logs.get(monitor)
if current is None:
warnings.warn(
'Early stopping conditioned on metric `%s` '
'which is not available. Available metrics are: %s' %
(monitor, ','.join(list(logs.keys()))), RuntimeWarning
)
return
if self.monitor_ops[i](current - self.min_deltas[i], self.bests[i]):
self.bests[i] = current
self.waits[i] = 0
reset_all_waits = True
else:
self.waits[i] += 1
if reset_all_waits:
for i in range(len(self.waits)):
self.waits[i] = 0
return
num_sat = 0
for wait in self.waits:
if wait >= self.patience:
num_sat += 1
if num_sat == len(self.waits):
self.stopped_epoch = epoch
self.model.stop_training = True
print(self.waits)
def on_train_end(self, logs=None):
if self.stopped_epoch > 0 and self.verbose > 0:
print('Epoch %05d: early stopping' % (self.stopped_epoch + 1))This is almost identical to the original EarlyStopping callback, except that it resets all counters if just a single quantity improves, and requires all quantities being tracked to simultaneously get worse in order for training to stop. I’ll note that this did not improve early stopping decision making much since there was a point quite early on during training where both loss and accuracy were getting worse. However, this callback is more lenient than the original, and does not assume a correlation between validation loss and accuracy, so that’s one less thing to worry about.
Conclusion
Early stopping is a coarse heuristic that requires clever tuning to prevent underfitting. The change that I proposed to it in this post is not a silver bullet, but it is a step in the right direction. The final piece of the puzzle is to change what is considered to be the best value seen thus far. The EarlyStopping callback compares current performance statistics to the best ones seen in the entire history of training the model. Perhaps this is not the best idea because we are likely more interested in performance trends than in a comparison against a single value.
I hope this post has increased your understanding of how early stopping works under the hood, how it can fail, and how it can be improved!
